The Golden Circle

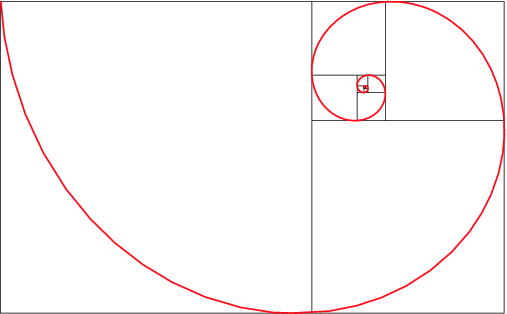
In chapter 4 of my book I talk about a rectangle inscribed within a circle. Naturally there are an indefinite number of such figures. Take the diagram on the right, kindly produced by Michael Schneider. Look at the outermost circle, and the largest rectangle that lies inside it, touching its circumference at A, B and C. You could move points A and B nearer to the left-hand end of the horizontal diameter of the large circle, or else push them further apart towards the two ends of the vertical diameter, producing an ever-thinner oblong shape. Halfway between these  extremes the rectangle would become a square. But the shape Michael has drawn is a Golden Rectangle, so we can call the whole figure a Golden Circle ("Golden" because of the presence of the Rectangle). The G.R. is famous for being the "most beautiful" of rectangles, possessing the peculiar property that its sides are in the ratio of 1 to Phi (1.618...), so that if you cut off a square portion what remains is a smaller Golden Rectangle - and so forth, forming a logarithmic spiral, as in the following image.

When I wrote the book I was intending to use the Golden Circle as a way of exploring the relationship between Pi and Phi, but I never got around to it. My reason for being intrigued is simple. What we learn from Simone Weil - and what she learned from the Greeks - is that geometry is full of theological meaning. We have forgotten how to make those connections. It is not that we can prove the Trinity or the Incarnation with diagrams, but that the mathematical world is full of analogies that echo theological and spiritual truth. You might even say that mathematical necessities are a portrait of divine freedom, since in God freedom and necessity coincide. The beauties of geometry and arithmetic are a world of metaphors and help to raise our minds towards the contemplation of divine truth. My book only touches on this, but a much fuller and richer account is given by Vance G. Morgan of Providence College in his book Weaving the World: Simone Weil on Science, Mathematics and Love, reviewed here.