The word tradition derives from trans- "over" and dare "to give". In every traditional society or civilization, a process takes place that can be called a “handing over” of the stories, the knowledge, the accumulated wisdom of one generation to the next. It is a handing over which makes each new generation into a source of wisdom for the one that will follow. What is handed over is a “gift”. It is not simply a bundle of property whose title deed is being transferred to the next generation. Rather, it carries within it something of the giver. Its transmission is an act of love. Thus the gift of tradition involves and transforms the interiority of both the giver and the recipient.
Tradition in the sense I am describing is of the highest value because it is not something we simply manufacture, nor something cooked up by our parents, but something our parents themselves have received with gratitude and respect. Its origin is what makes it sacred. Some kind of revelation of truth, or what is believed to be a revelation, forms the seed of every great tradition. Tradition is venerated because of this. The moment we suspect that our tradition is based on a lie is the moment it loses its authority over us. Thus tradition is based on the act of faith. I adhere not simply because it has been handed down to me, but because I believe it is “true” (even if I cannot directly verify its truth for myself).
The receptivity proper to love makes possible the transmission of tradition from one generation to the next. And when that spirit is present, tradition is never felt like a dead weight on the present. Only a tradition that has lost this spirit can become a deadening force.
Photograph of the Vatican Library by Br Lawrence Lew OP, used with permission.
Sunday 20 June 2010
Wednesday 16 June 2010
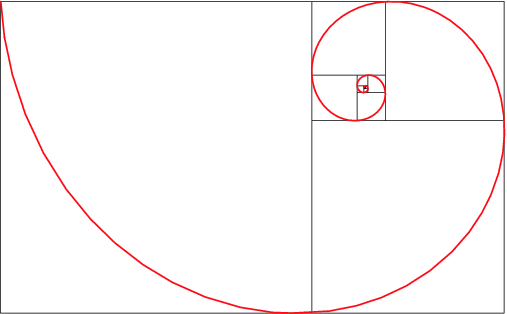
The Golden Circle
In chapter 4 of my book I talk about a rectangle inscribed within a circle. Naturally there are an indefinite number of such figures. Take the diagram on the right, kindly produced by Michael Schneider. Look at the outermost circle, and the largest rectangle that lies inside it, touching its circumference at A, B and C. You could move points A and B nearer to the left-hand end of the horizontal diameter of the large circle, or else push them further apart towards the two ends of the vertical diameter, producing an ever-thinner oblong shape. Halfway between these extremes the rectangle would become a square. But the shape Michael has drawn is a Golden Rectangle, so we can call the whole figure a Golden Circle ("Golden" because of the presence of the Rectangle). The G.R. is famous for being the "most beautiful" of rectangles, possessing the peculiar property that its sides are in the ratio of 1 to Phi (1.618...), so that if you cut off a square portion what remains is a smaller Golden Rectangle - and so forth, forming a logarithmic spiral, as in the following image.
When I wrote the book I was intending to use the Golden Circle as a way of exploring the relationship between Pi and Phi, but I never got around to it. My reason for being intrigued is simple. What we learn from Simone Weil - and what she learned from the Greeks - is that geometry is full of theological meaning. We have forgotten how to make those connections. It is not that we can prove the Trinity or the Incarnation with diagrams, but that the mathematical world is full of analogies that echo theological and spiritual truth. You might even say that mathematical necessities are a portrait of divine freedom, since in God freedom and necessity coincide. The beauties of geometry and arithmetic are a world of metaphors and help to raise our minds towards the contemplation of divine truth. My book only touches on this, but a much fuller and richer account is given by Vance G. Morgan of Providence College in his book Weaving the World: Simone Weil on Science, Mathematics and Love, reviewed here.
When I wrote the book I was intending to use the Golden Circle as a way of exploring the relationship between Pi and Phi, but I never got around to it. My reason for being intrigued is simple. What we learn from Simone Weil - and what she learned from the Greeks - is that geometry is full of theological meaning. We have forgotten how to make those connections. It is not that we can prove the Trinity or the Incarnation with diagrams, but that the mathematical world is full of analogies that echo theological and spiritual truth. You might even say that mathematical necessities are a portrait of divine freedom, since in God freedom and necessity coincide. The beauties of geometry and arithmetic are a world of metaphors and help to raise our minds towards the contemplation of divine truth. My book only touches on this, but a much fuller and richer account is given by Vance G. Morgan of Providence College in his book Weaving the World: Simone Weil on Science, Mathematics and Love, reviewed here.
Friday 4 June 2010
Analogy
The use of analogy is fundamental for human thought and language, and in particular for theology. Derived from the Greek analogia "proportion" (ana- "upon, according to" + logos "meaning" or "word"), it refers to the way we compare one thing with another on the basis of some likeness or similarity. It is more complicated than a simile, which happens when I straightforwardly compare one thing to another ("God is like a light"). It is also more complicated than a metaphor, which is when in poetic language I simply assume the similarity in the way I describe something ("God is a light for my eyes and a path for my feet").
An analogy is built out of similes and metaphors - it extends them not just to things but to relationships between things. If a simile is like a ratio (A : B), an analogy is a ratio of ratios (A:B : C:D, or "the relationship of A to B is like the relationship of C to D"). So to form an analogy we might say, for example, "Clay is to the potter as the world is to God". But "analogy" is also used more generally to cover all the ways we compare things that are similar to each other in some respect but not others. Everything we say about God relies on metaphor and analogy, because the words we use necessarily come from the things we can see and touch.*
So God-talk has to be taken with a pinch of salt. When we talk about God we mustn't take ourselves too literally. There is an analogy here with the problem of "graven images", or the temptation to mistake the image for what it represents. But what if God talks about God? In Jesus, we believe, God spoke as a man. Just as the Incarnation gave a justification for icons, so it gave a justification for saying certain things about God and believing them to be true. Philosophy and mysticism were possible before Christ - but now there is also theology. The things in the world were always "like" God in certain ways, not just as signs of his presence and activity but as expressions of his nature, or natural symbols of him. But now they can also be sacraments and sacramentals.
All of this perhaps serves as background to the use in my book of geometrical and mathematical "analogies" to the Trinity. Thomas Aquinas was perfectly clear on the fact that the Trinity cannot be proved by anything in nature - nevertheless, once we know by revelation that God is triune, we can see traces or impressions of the Trinity everywhere. So, for example, all things (1) subsist, (2) have a definite form, and (3) are ordered to an end (echoing Father, Son and Spirit). Following Simone Weil, I wanted to show that fundamental numbers and shapes also "echo" the Trinity in this way. There is no attempted proof here, just an intellectual intuition or an aid to contemplation, but the point is that knowledge of the Trinity enables us to appreciate the beauty of creation by seeing in its ordered harmony a meaning that we could not know before. Mathematics, in its own way (and you won't hear this said too often!), is a picture of love.
* There is much talk in theology about the "analogy of being", or attempts to compare the existence of God and that of the world. For an interesting discussion of that topic go here.
The photograph is by Tom Bree
Subscribe to:
Posts (Atom)